10 Solutions to Selected Exercises

1. Reason and Argument

Identify the premises and conclusion of each of the following arguments.
1. You did not turn the ignition. The car starts when you turn the ignition and the tank is full. But the tank is full and the car did not start.
2. If the mind is the same as the brain, then whatever is true of one is true of the other. The brain is a physically extended object but the mind is not. So, the mind is not the same as the brain.
  Solution:
  1. If the mind is the same as the brain, then whatever is true of one is true of the other.
  2. The brain is a physically extended object but the mind is not.
  3. The mind is not the same as the brain.
3. The deal will fall through unless Smith is part of the negotiation. So, the deal will not be completed. For Smith just phoned to let us know she cannot join the negotiation.
  Solution:
  1. The deal will fall through unless Smith is part of the negotiation.
  2. Smith just phoned to let us know she cannot join the negotiation.
  3. The deal will not be completed.
4. You will be admitted into the club just in case you apply for club membership and you are not perceived to be eager to join. Applying for club membership is regarded as a sign of eagerness. That is, if you apply for club membership, you will be perceived to be eager to join. So, you will not be admitted into the club.
  Solution:
  1. You will be admitted into the club just in case you apply for club membership and you are not perceived to be eager to join.
  2. If you apply for club membership, you will be perceived to be eager to join.
  3. You will not be admitted into the club.
Which of the following arguments are valid?
1. It today is Tuesday, then today is not Wednesday. Today is Tuesday. So, today is not Wednesday.
  Solution:
  This is a valid argument because it is an instance of a valid argument pattern:
  If \(p\), then not-\(q\)
  \(p\)
  Not-\(q\)
  and none of its instances has true premises and a false conclusion.
2. Today is Tuesday or Thursday. So, today is Tuesday Solution:
  This is not a valid argument because it is not an instance of a valid argument pattern. It is, for example, an instance of the pattern:
  \(p\) or \(q\)
  \(p\)
  To appreciate its invalidity, notice that there are instances with true premises and a false conclusion, e.g.
  Snow is black or snow is white (true)
  Snow is black (false).
3. Today is Tuesday or Thursday. Today is not Thursday. So, today is Tuesday
4. I’m late on Tuesdays. I’m late again today. So, today is Tuesday
Justify the invalidity of each of the argument patterns below by providing an instance with true premises and a false conclusion.
1. If \(p\), then \(q\) or \(r\).
  Not \(q\).
  Therefore, \(r\).
2. \(p\) unless \(q\).
  \(q\).
  \(p\).
  Solution:
  This is not a valid argument pattern because some of its instances have true premises and a false conclusion, e.g.,
  1. The commute to campus will take over an hour unless I find a way to live nearby campus. (true)
  2. I will find a way to live nearby campus (true)
  3.The commute to campus will take over an hour (false).
3. \(p\) if, and only if, both \(q\) and \(r\).
  \(r\).
  \(q\).
True or false? Justify your answers.
1. There are valid arguments with false premises and a true conclusion.
  Solution:
  This is true. The following is a valid argument with false premises and a true conclusion:
  1. Snow is white and snow is black (false)
  2. Snow is white (true).
  It is a valid argument because it is an instance of a valid argument pattern:
  \(p\) and \(q\).
  \(p\).
2. There are invalid arguments with true premises and a true conclusion.
3. There are valid arguments with a false conclusion.
4. There are sound arguments with a false conclusion.
  Solution:
  This is false: a sound argument is a valid argument with true premises. But if a valid argument has true premises, then it must have a true conclusion. It follows that a sound argument must have a true conclusion.
5. If an argument is valid, then at least one of its premises is true.
  Solution:
  This is false. The argument we deployed in response to part a has no true premises at all.

2. Propositional Logic

Add quotation marks to the following sentences in order to obtain a true sentence of Enlglish. If there is more than one solution, make sure to explain why.
1. Los Angeles names a city in Southern California.
2. Los is part of Los Angeles.
  Solution:
  ‘Los’ is part of ‘Los Angeles’
3. Snow is white is a grammatical sentence of English.
  Solution:
  ‘Snow is white’ is a grammatical sentence of English.
4. What is monosyllabic but whatever is polysyllabic.
  Solution:
  ‘What’ is monosyllabic but ‘whatever’ is polysyllabic..
Determine whether each of the following expressions is a sentence of propositional logic.
1. \(\neg \neg A\)
Solution:
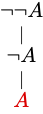⊕ No construction tree is available. This is not a sentence of propositional logic.
By rule 2, \(\neg \neg A\) is a sentence if \(\neg A\) is a sentence.
By rule 2, \(\neg A\) is a sentence if \(A\) is a sentence.
By rule 3, since \(A\) is not a propositional variable, \(A\) is not a sentence.
So, it follows that \(\neg \neg A\) is not a sentence.
1. \((p \to (\neg q))\)
2. \((p)\)
3. \((q \to (\neg \neg p \vee r))\)
Solution:
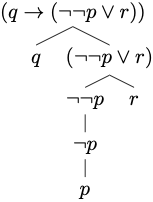⊕ A construction tree for the formula. This is a sentence of propositional logic.
By rule 2, \((q \to (\neg \neg p \vee r))\) is a sentence if both \(q\) and \((\neg \neg p \vee r)\) is a sentence.
By rule 1, \(q\) is a sentence.
By rule 2, \((\neg \neg p \vee r)\) is a sentence if both \(\neg \neg p\) and \(r\) are sentences.
By rule 2, \(\neg \neg p\) is a sentence if \(\neg p\) is a sentence.
By rule 2, \(\neg p\) is a sentence if \(p\) is a sentence.
By rule 1, both \(p\) and \(r\) are sentences.
So, we conclude that \((q \to (\neg \neg p \vee r))\) is a sentence.
Determine whether each of the following expressions is an abbreviation for a sentence of propositional logic.
1. \(p \to (q \wedge r)\)
  Solution:
  By convention 3, this is an abbreviation for \((p \to (q \wedge r))\).
2. \(p \to q \to r\)
3. \(p \vee (q \wedge r)\)
4. \(p \to (q\wedge r \to q)\)
Use the truth table method to determine whether each of the following formulas is a tautology, a contradiction, or neither a tautology or a contradiction.
1. \(((p \vee q) \to \neg (p \to q))\)
  Solution:
  This sentence is neither a tautology nor a contradiction because it is true under some assignments, e.g., rows 2 and 4, and false under others, e.g., rows 1 and 3. \[ \begin{array}{|c|c|c|c|c|} \hline p & q & (p \vee q) & \neg (p \to q) & ((p \vee q) \to \neg (p \to q)) \\ \hline T & T & T & F &\color{red}{F} \\ T & F & T & T & \color{red}{T}\\ F & T & T & F & \color{red}{F}\\ F & F & F & F & \color{red}{T} \\ \hline \end{array} \]
2. \(p \to (q \to p)\)
3. \(q \to (q \to p)\)
Use the truth table method to determine whether the following pairs of sentences are logically equivalent.
1. \(p \to q\), \(q \wedge \neg (p \vee q)\)
2. \(p \to p\), \(q \to q\)
  Solution:
  These sentence are logically equivalent because they have the same truth value under every assignment. \[ \begin{array}{|c|c|c|c|} \hline p & q & p \to p & q \to q \\ \hline T & T & T & T \\ T & F & T & T \\ F & T & T & T \\ F & F & T & T \\ \hline \end{array} \]
Use the truth table method to determine whether the following sets of sentences are consistent.
1. \(\{ p, q, \neg (p \wedge q)\}\)
2. \(\{p \vee q, q \to r, \neg (p \wedge r)\}\)
  Solution:
  This is a consistent set of sentences, since every sentence in the set is true under some assignments, e.g., rows 4 and 5. \[ \begin{array}{|c|c|c|c|c|c|} \hline p & q & r & p \vee q & q \to r & \neg (p \wedge r) \\ \hline T & T & T & T & T & F\\ T & T & F & T & F & T\\ T & F & T & T & T & F\\ T & F & F & \color{red}{T} & \color{red}{T} & \color{red}{T}\\ F & T & T & \color{red}{T} & \color{red}{T} & \color{red}{T}\\ F & T & F & T & F & T\\ F & F & T & F & T & T\\ F & F & F & F & T & T\\ \hline \end{array} \]
Use the truth table method to determine whether the following arguments are valid.
1. \(p \to q\)
  \(q \to r\)
  \(r\)
2. \(q \vee (p \wedge r)\)
  \(\neg q\)
  \(r\)
  Solution:
  This argument is valid since there is no assignment, that is, no row of the truth table, on which the premises come out true and the conclusion false: \[ \begin{array}{|c|c|c|c|c|c|} \hline p & q & r &q \vee (p \wedge r) & \neg q & r \\ \hline T & T & T & T & F & T\\ T & T & F & T & F & F\\ T & F & T & T & T & T\\ T & F & F & F & T & F\\ F & T & T & T & F & T\\ F & T & F & T & F & F\\ F & F & T & F & T & T\\ F & F & F & F & T & F\\ \hline \end{array} \]
Use the search-for-counterexample method to determine whether the following arguments are valid.
1. \(p \to (q \vee r)\)
  \(r \to (p \to q)\)
  \(p\)
  \(q\)
  Solution:
  The argument is invalid, since we are able to build an assignment under which the premises come out true and the conclusion false, e.g., one on which \(p\) is true but both \(q\) and \(r\) are false. \[ \begin{array}{|c|c|c|c|c|c|c|} \hline p & q & r &p \to (q \vee r) & r \to (p \to q) & p & q \\ \hline T & F & F & \color{red}{T} & \color{red}{T} & \color{red}{T} & \color{red}{F} \\ \hline \end{array} \]
2. \((p \to q) \wedge (q \to p)\)
  \(\neg (p \wedge r)\)
  \(\neg (r \to s)\)
  \(s \to q\)

3. Translation into Propositional Logic

Translate the following sentences into the language of propositional logic.
1. If interest rates fall, then we will be able to borrow more money and inflation will rise.
  Solution:
  ⊕Translation key
  \(p\): Interest rates fall.
  \(q\): We will be able to borrow more money.
  \(r\): Inflation will rise.
  We proceed in three steps:
  
  If interest rates fall, then (we will be able to borrow more money and inflation will rise)
  
  Interest rates fall \(\to\) (we will be able to borrow more money \(\wedge\) inflation will rise)
  
  \(p \to (q \wedge r)\)
2. Your computer will not start unless you turn it on and the battery is fully charged.
3. The mayor’s office made the decision, even though it did not sit well with its constituents.
4. You will carry an umbrella outside just in case it is raining or you are under the impression that it is raining.
  Solution:
  ⊕Translation key
  \(p\): Interest rates fall.
  \(q\): We will be able to borrow more money.
  \(r\): Inflation will rise.
  We proceed in three steps:
  
  You carry an umbrella outside if, and only if, (it is raining or you are under the impression that it is raining)
  
  You carry an umbrella outside \(\leftrightarrow\) (it is raining \(\vee\) you are under the impression that it is raining)
  
  \(p \leftrightarrow (q \vee r)\)
5. The deal will be completed if all parties agree to it and the deal is found to be in compliance with current regulations.
Assess the following arguments for propositional validity.
1. The car will not start unless you turn the ignition and press the accelerator. You turned the ignition but the car failed to start. So, you did not press the accelerator.
  Solution:
  First, we rephrase the argument in premise conclusion form:
  
  1. If it is not the case that you turn the ignition and press the accelerator, then the car will not start.
  
  2. You turned the ignition and the car did not start.
  
  3. You did not press the accelerator.
  
  Second, we translate the argument into the language of propositional logic:
  
  1. \(\neg (p \wedge q) \to \neg r\)
  
  2. \(p \wedge \neg r\)
  
  3. \(\neg q\)
  
  Third, we use the search for counterexample method to check whether there is an assignment on which the premises come out true and the conclusion false: \[ \begin{array}{|c|c|c|c|c|c|} \hline p & q & r &\neg (p \wedge q) \to \neg r & p \wedge \neg r & \neg q \\ \hline T & T & F & T & T & F \\ \hline \end{array} \] Since we have identified one such assignment, we conclude that the argument is propositionally invalid.
2. The mind is a simple substance only if it is not made of further parts. If the mind is material, then it is is made of further parts. So, if the mind is a simple substance, then it is not material.
3. My client is not the burglar. For the doors show no signs of forced entry. If the doors show no signs of forced entry, then if my client is the burglar, he must have climbed to the unlocked window on the second floor. However, my client is arthritic and could not climb to that unlocked window on the second floor.
4. If the British are coming, then they are coming by land or by sea. Paul Revere will light only one lamp, if they are coming by land. He will light two lamps, if they are coming by sea. Paul Revere will light only one lamp. So, the British are coming.
5. The insurance company will cover your expenses only if you are current with your monthly payments. But if you are current with your monthly payments, then you can afford to cover the expenses yourself. So, the insurance company will not cover your expenses unless you can afford to cover them yourself.
  Solution:
  First, we rephrase the argument in premise conclusion form:
  
  1. The insurance company will cover your expenses only if you are current with your monthly payments.
  
  2. If you are current with your monthly payments, then you can afford to cover the expenses yourself.
  
  3. The insurance company will not cover your expenses unless you can afford to cover them yourself.
  
  Second, we translate the argument into the language of propositional logic:
  
  1. \(p \to q\)
  
  2. \(q \to r\)
  
  3. \(\neg r \to \neg p\)
  
  Third, we use the search for counterexample method to check whether there is an assignment on which the premises come out true and the conclusion false: \[ \begin{array}{|c|c|c|c|c|c|} \hline p & q & r &p \to q & q \to r & \neg r \to \neg p \\ \hline T & T & F & T & ! & F \\ \hline \end{array} \] Since no such assignment exists, we conclude that the argument is propositionally valid.

4. Natural Deduction for Propositional Logic

Provide a natural deduction proof in order to justify each of the claims below:
1. \(p, \neg q \vdash p \to (\neg q \vee r)\)
  Solution:
2. \(p \leftrightarrow (q \vee r), \neg q, \neg r \vdash \neg p\)
3. \(p \to \neg(q \wedge r), q, \neg r \to \neg q \vdash \neg p\)
  Solution:
4. \(p \leftrightarrow q, q \vee r, r \to (p \vee q) \vdash q\)
5. \((p \wedge q) \leftrightarrow (q \vee r), \neg r \to (\neg p \to q) \vdash p\)
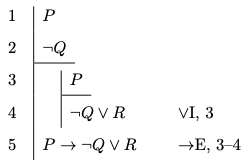
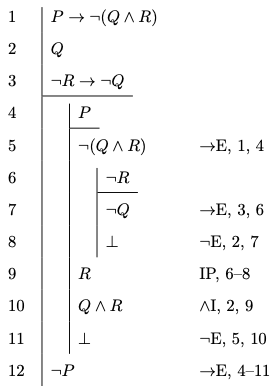
  Solution:

5. Natural Language and Propositional Logic

Determine whether the following English sentences are tautologies, contradictions, or neither tautologies nor contradictions:
1. Someone is a logician and not a logician.
  Solution:
  We translate the sentence into the language of propositional logic:
  \(p\)
  Translation key:
  \(p\): Someone is a logician and not a logician.
  
  There is a simple an assignment on the sentence is false: \[ \begin{array}{|c|c|c|c|c|c|} \hline p & p\\ \hline F & F \\ \hline \end{array} \] We conclude it is not a logical truth.
2. Some logicians are philosophers but some logicians are not philosophers.
3. If all logicians are philosophers, then if some philosophers are logicians, then all logicians are philosophers.
4. Someone is a logician and someone is not a logician.
  Solution:
  We translate the sentence into the language of propositional logic:
  \(p \wedge q\)
  Translation key:
  \(p\): Someone is a logician.
  \(q\): Someone is not a logician.
  
  There is a simple an assignment on the sentence is false: \[ \begin{array}{|c|c|c|c|c|c|} \hline p & q & p \wedge q\\ \hline F & F & F \\ \hline \end{array} \] We conclude it is not a logical truth.
5. All logicians are philosophers but no philosophers are logicians.
Determine whether the following arguments are propositionally valid:
1. The deal will be completed only if Smith or Jones are in attendance. If Smith attends, then Jones will too. Jones will not be in attendance. Therefore, the deal will not be completed.
  Solution:
  First, we rephrase the argument in premise conclusion form:
  1. The deal will be completed only if Smith or Jones are in attendance.
  2. If Smith attends, then Jones will too.
  3. Jones will not be in attendance.
  4. The deal will not be completed.
  
  Second, we translate the argument into the language of propositional logic:
  1. \(p \to (q_1 \vee q_2)\)
  2. \(q_1 \to q_2\)
  3. \(\neg q_2\)
  4. \(\neg p\).
  Translation key:
  \(p\): The deal will be completed.
  \(q_1\): Smith is in attendance.
  \(q_2\): Jones is in attendance.
  
  Third, we use the search for counterexample method to check whether there is an assignment on which the premises come out true and the conclusion false: \[ \begin{array}{|c|c|c|c|c|c|} \hline p & q_1 & q_2 & p \to (q_1 \vee q_2) & q_1 \to q_2 & \neg q_2 & \neg p \\ \hline T & F & F & ! & T & T & F \\ \hline \end{array} \] Since there is no assignment on which the premises come out true and the conclusion false, we conclude that the argument is propositionally valid.
2. All logicians are philosophers. All logicians learn propositional logic at some point. So, some philosophers learn propositional logic at some point.
  Solution:
  First, we rephrase the argument in premise conclusion form:
  1. All logicians are philosophers.
  2. All logicians learn propositional logic at some point.
  3. Some philosophers learn propositional logic at some point.
  
  Second, we translate the argument into the language of propositional logic:
  1. \(p\)
  2. \(q\)
  3. \(r\)
  Translation key:
  \(p\): All logicians are philosophers.
  \(q\): All logicians learn propositional logic at some point.
  \(r\): Some philosophers learn propositional logic at some point.
  
  Third, we note that there is a simple an assignment on which the premises come out true and the conclusion false: \[ \begin{array}{|c|c|c|c|c|c|} \hline p & q & r & p & q & r\\ \hline T & T & F & T & T & F \\ \hline \end{array} \]
3. The deal will not be completed unless someone is in attendance. Neither Smith nor Jones will be in attendance. Therefore, the deall will not be completed.
Identify occurrences of designators, predicates, and quantifier expressions in the following sentences:
1. USC is located in Los Angeles.
  Solution:
  \(\underbrace{\text{USC}}_{\text{designator}}\) \(\underbrace{\text{is located in}}_{\text{predicate}}\) \(\underbrace{\text{Los Angeles}}_{\text{designator}}\)
2. Some private university is located in NYC.
3. Some critic admires every critic.
  Solution:
  \(\underbrace{\text{Some critic}}_{\text{quantifier phrase}}\) \(\underbrace{\text{admires}}_{\text{predicate}}\) \(\underbrace{\text{every critic}}_{\text{quantifier phrase}}\)
4. Mark Twain wrote Tom Sawyer.
5. Every students owns a computer.
  Solution:
  \(\underbrace{\text{Every student}}_{\text{quantifier phrase}}\) \(\underbrace{\text{owns}}_{\text{predicate}}\) \(\underbrace{\text{a computer}}_{\text{quantifier phrase}}\)
6. Everyone admires someone.
7. Some workday comes after a weekend day.
  Solution:
  \(\underbrace{\text{Some workday}}_{\text{quantifier phrase}}\) \(\underbrace{\text{comes after}}_{\text{predicate}}\) \(\underbrace{\text{a weekend day}}_{\text{quantifier phrase}}\)

6. Quantificational Logic

Determine whether each of the following expressions is an atomic formula of quantificational logic.
1. \(\neg R^2(x,y)\)
2. \(R^2(x,y)\)
3. \(A^3(a,b,x)\)
  Solution:
  This is an atomic formula of quantificational logic.
  \(A^3\) is a three-place predicate and while \(a\) and \(b\) are constants, \(x\) is a variable.
4. \(Q^1(e)\)
5. \(P^4(x,y,z,a)\)
6. \(R^2(P^1,a)\)
  Solution:
  This is not an atomic formula of quantificational logic.
  \(R^2\) is a two-place predicate but \(P^1\) is neither a constant nor a variable.
Determine whether each of the following expressions is a formula of quantificational logic.
1. \(\neg \neg R^2(x,y)\)
2. \((P^1(a) \to (A^2(x,y) \wedge \exists x Q^1(x))\)
  Solution:
  This is a formula of quantificational logic.
  By rule 2, \((P^1(a) \to (A^2(x,y) \wedge \exists x Q^1(x))\) is a formula if \(P^1(a)\) and \((A^2(x,y) \wedge \exists x Q^1(x))\) are each a formula.
  By rule 1, \(P^1(a)\) is a formula because it is an atomic formula.
  By rule 2, \((P^1(a) \to (A^2(x,y) \wedge \exists x Q^1(x))\) is a formula if both \(A^2(x,y)\) and \(\exists x Q^1(x)\) are formulas.
  By rule 1, \(A^2(x,y)\) is a formula because it is an atomic formula.
  By rule 3, \(\exists x Q^1(x)\) is a formula if \(Q^1(x)\) is a formula.
  By rule 1, both \(Q^1(x)\) is a formula because it is an atomic formula.
  So, we conclude that \((P^1(a) \to (A^2(x,y) \wedge \exists x Q^1(x))\) is a formula.
3. \(\forall x R^2(y,y)\)
4. \(\exists x y (P^1 \wedge P^1(y))\)
5. \(\forall \forall x R^2(y,x)\)
  Solution:
  This is not a formula of quantificational logic.
  It is neither an atomic formula nor a negation, conjunction, disjunction, conditional or biconditional. It is finally not of the form \(\forall v \varphi\) as the first quantifier is not followed by a variable. By rule 4, we conclude that it is not a formula of quantificational logic.
6. \(\exists x \exists y R(x,y)\)
Determine whether each of the following expressions is an abbreviation for a formula of quantificational logic.
1. \(\exists x \exists y R(x,y) \to P(x)\)
  Solution:
  This is an abbreviation for the formula \((\exists x \exists y R^2(x,y) \to P^1(x))\).
2. \(\forall x R(x) \vee \exists y Q(y,y)\)
3. \(P^1(x) \wedge Q^1(x) \vee R^2(x,y)\)
  Solution:
  This is not an abbreviation for a formula of quantificational logic.
4. \(P^1(x) \wedge Q^1(x) \to R^2(x,y)\)
5. \(\exists x P(x) \wedge \exists y Q(y) \wedge \exists z R(z)\)
6. \(\exists x \forall y \exists z (P(x) \wedge Q(y) \wedge R(x,y,z))\)
  Solution:
  This is an abbreviation for the formula \(\exists x \forall y \exists z ((P^1(x) \wedge Q^1(y) \wedge R^3(x,y,z))\).
Determine whether the following formulas contain a free occurrence of the variable \(x\).
1. \(\forall x (R(x,y) \wedge R(y,x))\)
2. \(\forall x R(x,y) \wedge R(y,x)\)
  Solution:
  By rule 1, the occurrence of \(x\) in \(R(y,x)\) is free.
  By rule 2, the occurrence of \(x\) in \(R(y,x)\) remains free in the conjunction \(\forall x R(x,y) \wedge R(y,x)\).
3. \((\exists x (P(x) \wedge Q(x)) \to \forall y R(x,y))\)
  Solution:
  By rule 1, the occurrence of \(x\) in \(R(x,y)\) is free.
  By rule 2, the occurrence of \(x\) in \(\forall y R(x,y)\) remains free in the conditional \(\exists x (P(x) \wedge Q(x) \to \forall y R(x,y)\).
4. \(\forall x \exists y R(x,y) \to \exists x \forall y R(y,x)\)
5. \((\forall x \exists y R(x,y) \to \forall y R(y,x))\)
6. \(\forall x (\exists y R(x,y) \to \forall y R(y,x))\)
Determine whether the following formulas are open or closed. Justify your answers.
1. \(\forall x R(x,y) \wedge R(y,x,z)\)
  Solution:
  This is an open formula as the occurrences of the variables \(y\) and \(z\) as well as the last occurrence of the variable \(x\) are all free.
2. \(R(a,b)\)
  Solution:
  This is a closed formula, since no variables occur, much less freely, in it.
3. \((\exists x (P(a,x) \wedge Q(x,a)) \to \forall y R(x,y))\)
4. \(\forall x R(y,y)\)
  Solution:
  This is an open formula as the two occurrences of the variables \(y\) both free.
5. \(\forall x \exists y \forall z R(x,y,x)\)
6. \((R(a,x) \to \forall x R(x,x))\)
Determine which of the following formulas are true in the following model:

\(D = \{p_1, p_2, p_3, p_4\}\)
\(a : p_1\)
\(b : p_2\)
\(P_1 : \text{enclosed by a circle}\)
\(Q : \text{enclosed by a dark grey figure}\)
\(P_2: \text{enclosed by a diamond}\)
\(R : \text{points to}\)
1. \(R(a,b)\)
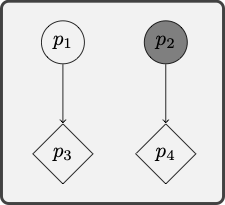
  Solution:
  This not true in the model because it is true relative to all assignments. Whatever the assignment, the denotation of \(a\) in the model, i.e., \(p_1\), does not point to the denotation of \(b\) in the model, i.e., \(p_2\).
2. \(R(a,b) \to R(b,b)\)
3. \(P(a) \wedge Q(b)\)
4. \(\exists x P_1(x) \wedge \exists x P_2(x)\)
5. \(\forall x (\exists y R(x,y) \vee \exists y R(y,x))\)
  Solution:
  This formula is true in the model because it is true relative to all assignments. Given an assignment \(\alpha\), we verify that for every \(p \in D\), the formula \(\exists y R(x,y) \vee \exists y R(y,x)\) is true relative to \(\alpha[x/p]\). There are four cases to consider:
  \(\alpha[x/p_1]\): \(\exists y R(x,y)\) is true in the model relative to this assignment because there is a member of the domain, \(p_3\), such that \(R(x,y)\) is true relative to the assignment \(\alpha[x/p_1][y/p_3]\). This is because the denotation of \(x\) relative to this assignment, \(p_1\), points to the denotation of \(y\) under the assignment, \(p_3\). Therefore, the disjunction \(\exists y R(x,y) \vee \exists y R(y,x)\) is true relative to \(\alpha[x/p_1]\).
  \(\alpha[x/p_2]\): \(\exists y R(x,y)\) is true in the model relative to this assignment because there is a member of the domain, \(p_4\), such that \(R(x,y)\) is true relative to the assignment \(\alpha[x/p_2][y/p_4]\). This is because the denotation of \(x\) relative to this assignment, \(p_2\), points to the denotation of \(y\) under the assignment, \(p_4\). Therefore, the disjunction \(\exists y R(x,y) \vee \exists y R(y,x)\) is true relative to \(\alpha[x/p_2]\).
  \(\alpha[x/p_3]\): \(\exists y R(y,x)\) is true in the model relative to this assignment because there is a member of the domain, \(p_1\), such that \(R(y,x)\) is true relative to the assignment \(\alpha[x/p_3][y/p_1]\). This is because the denotation of \(y\) relative to this assignment, \(p_1\), points to the denotation of \(x\) under the assignment, \(p_3\). Therefore, the disjunction \(\exists y R(x,y) \vee \exists y R(y,x)\) is true relative to \(\alpha[x/p_3]\).
  \(\alpha[x/p_4]\): \(\exists y R(y,x)\) is true in the model relative to this assignment because there is a member of the domain, \(p_2\), such that \(R(y,x)\) is true relative to the assignment \(\alpha[x/p_4][y/p_2]\). This is because the denotation of \(y\) relative to this assignment, \(p_2\), points to the denotation of \(x\) under the assignment, \(p_4\). Therefore, the disjunction \(\exists y R(x,y) \vee \exists y R(y,x)\) is true relative to \(\alpha[x/p_4]\).
6. \(\forall x (P_1(x) \to \exists y (Q(y) \wedge R(x,y)))\)

7. Translation into Quantificational Logic

Translate the following sentences into the language of quantificational logic.
1. Some Trojans fear Achilles, but Achilles fears every Trojan.
  Solution:
  \[ \exists x (P(x) \wedge R(x,a)) \wedge \forall x (P(x) \to R(a,x)) \] Translation key:
  \(a\): Achiles
  \(P\): Trojan
  \(R\): fears
2. All Trojans are courageous.
  Solution:
  \[ \forall x (P(x) \to Q(x)) \] Translation key:
  \(P\): Trojan
  \(Q\): courageous.
3. Only Trojans come from Troy.
  Solution:
  \[ \forall x (R(x,a) \to P(x)) \] Translation key:
  \(a\): Troy
  \(P\): Trojan
  \(R\): comes from
4. No Greek comes from Troy.
5. Achilles fears Paris, but Paris fears no one.
  Solution:
  \[ R(a,b) \wedge \forall x \neg R(b,x) \] Translation key:
  \(a\): Achiles
  \(b\): Paris
  \(R\): fears
6. Some Greeks fears some Trojans, and some Trojans fear some Greeks.
Assess the following arguments for quantificational validity.
1. All poisonous frogs are amphibians. Kermit is a poisonous amphibian. Therefore, Kermit is a frog.
  Solution:
  The argument is quantificationally invalid.
  1. \(\forall x ((P(x) \wedge Q(x)) \to R(x))\)
  2. \(P(a) \wedge R(a)\)
  3. \(Q(a)\)
  Translation key:
  \(a\): Kermit
  \(P\): poisonous
  \(Q\): frog
  \(R\): amphibian
  The following model makes the premises true and the conclusion false.
  
  \(D\): \(\{p_1, p_2\}\)
  \(a\): \(p_1\)
  \(P\): enclosed by a circle
  \(Q\): enclosed by a diamond
  \(R\): grey
2. Aristotle admired anyone who taught for free. Socrates taught for free, but no sophist did ever teach for free. So, Aristotle did not admire a sophist.
3. No weekday comes after Saturday. Monday is a weekday, but Sunday is not. Therefore, Monday does not come after Sunday.
  Solution:
  The argument is quantificationally invalid.
  1. \(\forall x (P(x) \to \neg R(x,a))\)
  2. \(P(b) \wedge \neg P(c)\)
  3. \(\neg R(c,b)\)
  Translation key:
  \(a\): Saturday
  \(b\): Monday
  \(c\): Sunday
  \(P\): weekday
  \(R\): comes after
  The following model makes the premises true and the conclusion false.
  
  \(D\): \(\{p_1, p_2, p_3\}\)
  \(a\): \(p_1\)
  \(P\): enclosed by a circle
  \(R\): points to
4. Some cube is green all over and some cube is red all over. No cube is both green all over and red all over. Some sphere is green all over. So, some sphere is not red all over.
5. No Trojan fears Achilles, but Achilles fears some Trojans. Paris is a Trojan. So, Achilles fears Paris but Paris does not fear Achilles.
  Solution:
  The argument is quantificationally invalid.
  1. \(\forall x (P(x) \to \neg R(x,a)) \wedge \exists x (P(x) \wedge R(a,x))\)
  2. \(P(b)\)
  3. \(R(a,b) \wedge \neg R(b,a)\)
  Translation key:
  \(a\): Achilles
  \(b\): Paris
  \(P^1\): Trojan
  \(R^2\): fears
  
  The following model makes the premises true and the conclusion false.
  
  \(D\): \(\{p_1, p_2\}\)
  \(a\): \(p_1\)
  \(b\): \(p_2\)
  \(P\): enclosed by a circle
  \(R\): points to
6. Some stadium is close to University Park. The Coliseum is a stadium. Therefore, the Coliseum is close to University Park.
7. Los Angeles is connected by direct flight to London. London is connected by direct flight to every major European city. Barcelona is a major European city. Therefore, Los Angeles is connected by direct flight to Barcelona.
  Solution:
  The argument is quantificationally invalid.
  1. \(R(a,b)\)
  2. \(\forall x (P(x) \to R(b,x))\)
  3. \(P(c)\)
  4. \(R(a,c)\)
  Translation key:
  \(a\): Los Angeles
  \(b\): London
  \(c\): Barcelona
  \(P\): major European city
  \(R\): connected by direct flight
  
  The following model makes the premises true and the conclusion false.
  
  \(D\): \(\{p_1, p_2, p_3\}\)
  \(a\): \(p_1\)
  \(b\): \(p_2\)
  \(c\): \(p_3\)
  \(P\): enclosed by a circle
  \(R\): points to
8. All Greeks feared Hector or Paris. Paris feared no Greek who feared Hector. Therefore, some Greeks feared Paris.

8. Natural Deduction for Quantificational Logic

Provide a natural deduction proof in order to justify each of the claims below:
1. \(\exists x P(x) \to \exists x Q(x), \forall x P(x) \vdash \exists x Q(x)\)
2. \(\exists x P(x) \wedge \exists x Q(x), \neg \exists x(P(x) \wedge Q(x)), \forall x (R(x) \to P(x)) \vdash \exists x \neg R(x)\)
  Solution:
3. \(\forall x (P(x) \to \neg Q(x)), \forall x (R(x) \to Q(x)) \vdash \forall x (R(x) \to \neg P(x))\)
4. \(\forall x (P(x) \to (\exists y R(x,y) \to Q(x))), \neg \exists y Q(y) \vdash \forall y (P(y) \to \forall z \neg R(y,z))\)
  Solution:
5. \(\forall x (P(x) \to \forall y (R(x,y) \to P(y))), \exists x (Q(x) \wedge P(x)) \vdash \exists x (Q(x) \wedge \forall y (R(x,y) \to P(y)))\)
  Solution:

10. Identity

For each set of formulas below, find a model we can use to justify the fact that the set is consistent. Please justify your answers.
1. \(\{\forall x (P(x) \leftrightarrow Q(x)), P(a), Q(b), \neg a = b\}\)
2. \(\{\forall x (R(a,x) \to R(b,x), \neg R(a,a), R(b,a) \}\)
For each argument below, find a model we can use to justify the fact that the argument is invalid. Please justify your answers.
1. \(\forall x (P(x) \to Q(x)), \neg Q(a) \vdash a = b \to R(a,b)\)
2. \(\exists x P(x), \exists x Q(x) \vdash \exists x \exists y \neg x = y\)
Provide a natural deduction proof to justify each of the claims below:
1. \(\forall x (P(x) \to Q(x)), \neg Q(a), P(b) \vdash a = b \to R(a,b)\)
2. \(\exists x \forall y (P(x) \leftrightarrow y = x), P(a) \vdash \forall x (P(x) \to x = a)\)
3. \(\exists x P(x), \exists x Q(x), \neg \exists x (P(x) \wedge Q(x)) \vdash \exists x \exists y \neg x = y\)