6 Formal Language
The language of quantificational logic will afford the means to capture the validity of a variety of arguments for which propositional logic appears to be inadequate. We specify:
a syntax for the language, which will include a vocabulary and a set of grammatical rules designed to specify which expressions are formulas of the language, and
a semantics for the language, which will explain how to interpret the expressions and formulas of the language and define what is for a formula to be true under a given interpretation.
Syntax
We begin with the vocabulary of quantificational logic.
Vocabulary
The vocabulary of quantificational logic contains six types of symbol:
- Constants
-
These are the lowercase letters
- Predicates
-
These are uppercase letters
- Variables
-
These are lowercase letters
- Connectives
-
These are the symbols:
- Quantifiers
-
There are two quantifier expressions:
-
There are two parentheses:
-
Nothing else is a symbol of the language.
Grammar
The grammar of quantificational logic explains how to combine these symbols into formulas of the language. We proceed in two stages.
- Atomic Formula
-
If
Atomic formulas are the formal counterparts of simple predications such as ‘Los Angeles is a city’ or ‘Los Angeles is between San Diego and San Francisco’.
Example 6.1 Each of the expressions below is an atomic formula of quantificational logic:
Atomic formulas provide simple constituents for more complex formulas.
- Formula
-
We now define what is for an expression to be a formula of quantificational logic.
- All atomic formulas are formulas.
- If
- If
- Nothing else is a formula.
We proceed to illustrate the characterization of formula through concrete examples.
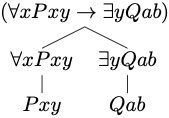 The construction tree depicts the construction of the formula from
simpler constituents.
The construction tree depicts the construction of the formula from
simpler constituents.
Example 6.2 The expression below is a formula of quantificational logic:
- By rule 2,
- By rule 3,
- By rule 3,
- By rule 1, each
Therefore, we conclude that
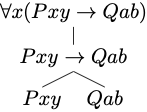 The construction tree depicts the construction of the formula from
simpler constituents.
The construction tree depicts the construction of the formula from
simpler constituents.
Example 6.3 The expression below is a formula of quantificational logic:
- By rule 3,
- By rule 2,
- By rule 1, each
Therefore, we conclude that
We now make a distinction between two types of occurrences of a variable in a formula. In the formula
Free Occurrences
- Free Occurrence of a Variable
-
We define what is for an occurrence of a variable to be free in a formula:
- All occurrences of a variable in an atomic formula are free.
- The free occurrences of a variable in formulas of the form
- No occurrence of the variable
Example 6.4 The first two occurrences of the variable
By rule 1,
By rule 1,
By rule 2, the last two occurrences of
An occurrence of a variable is free when it has not been captured by a quantifier. In the last example, the last two occurrences of the variable
Bound Occurrences
- Bound Occurrence of a Variable:
-
An occurrence of a variable in a formula is bound if, and only if, it is not free in that formula.
A variable occurs freely in a formula if, and only if, some of its occurrences in the formula are free.
Open and Closed Formulas
- Open and Closed Formulas
-
A formula is open if, and only if, some variables occur freely in the formula. Otherwise, the formula is closed.
Example 6.5 The formula below is open:
Example 6.6 The formula below is closed:
- Notational Convention
-
We may remove the outer parentheses from a formula that is not part of another formula.
Notice that this convention will not allow us to omit the parentheses in a formula such as:
Example 6.7 We are able to use the expression
Semantics
We now explain how to interpret the language of quantificational logic. We will not use assignments of truth values to interpret the language but rather models, which will assign a semantic value to the simplest constituents of a formula. A model for quantificational logic includes:
- a domain of discourse for the quantifiers to range over,
- a specification of denotations for the constants of the language, and
- a specification of extensions for the predicates of the language
The domain of discourse determines the truth conditions of quantified formulas in much the way in which the truth value of a natural language sentence such as ‘I packed everything into my suitcase’ depends on what is the domain of objects over which we take the quantifier ‘everything’ to range. In what follows, we will use a non-empty set of objects as the domain of a model. There are no restrictions on the domain of discourse other than it must contain at least one object.
We will let a model specify denotations for the constants of the language. Constants are formal counterparts of names in natural language, which are generally taken to denote an object in the domain of discourse, e.g., ‘Los Angeles’ denotes a city in Southern California, and ‘Silver Lake’ denotes an area of Los Angeles. A model will assign a member of the domain to each constant of the language as a denotation.
The case of predicates is more subtle. Predicates are formal counterparts of predicate expressions in natural language, which are true of some objects and not of others. Let us begin with one-place predicates such as ‘is red’, which applies to red objects and does not apply to non-red objects. One suggestion at this point is to identify the interpretation of ‘red’ with the set of objects to which the predicate applies. The set of objects to which a given predicate applies is known as the extension of the predicate. Thus the extension of the predicate ‘red’ is the set of red objects and the extension of the predicate ‘human being’ is the set of human beings.
The case of two-place predicates is more complicated. The predicate ‘is south of’ applies to Los Angeles and San Francisco in that order but it fails to apply to San Francisco and Los Angeles in that order. This raises the question of how to specify the extension of the predicate. The answer is to use sets of ordered pairs of objects in the domain, e.g.,
Model
- Model
-
A model
- If
- If
- If
- If
Given an argument in the language of quantificational logic, we will often consider the question of whether there is an interpretation of the language on which the premises are true and the conclusion false. That amounts to the question whether there is a model for quantificational logic, which verifies the premises but not the conclusion of the argument.
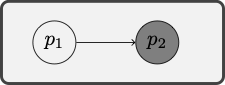
Example 6.8 Consider the argument given below.
We may evaluate the premises and conclusion of the argument in a model
We will eventually explain that the model verifies the premises but not the conclusion of the argument.
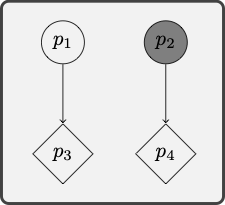
One heuristic you may find helpful for the specification of a model is to use a diagrams as partial representation of the model. The diagram should come accompanied with a key designed to help us specify the interpretation of the relevant constants and predicates.
Example 6.9 The diagram included in the margin encodes the partial specification of a model
Notice that the diagram comes with a key designed to explain how to interpret each predicate and constant in the diagram.
This heuristic comes with severe limitations, since some models, e.g., models with an infinite domain, are much too complex to be represented by means of a finite diagram. The method will, however, suffice for some purposes; it will enable us to establish the invalidity of a broad family of arguments in quantificational logic.
The definition of a model makes sure that models provide a semantic value for constants and predicates, but they remain silent when it comes to variables. If constants are the formal counterparts of names in natural language, variables resemble pronouns like ‘he’ or ‘she’, which do not appear to receive a denotation when used in a sentence like ‘If a person likes opera, then she likes classical music.’ For this reason, models do not assign a denotation to variables.
Instead, variables will be treated as temporary labels for members of the domain. That will allow us to evaluate an open formula
- Variable Assignment
-
A variable assignment
Example 6.10 Each of the maps depicted below are variable assignments over a model
Once variable assignments are in place, we are in a position to assign a semantic value to a variable
For technical reasons, we want to assign semantic values to open formulas in a model relative to a variable assignment over the model. The definition of truth in a model relative to a variable assignment will be inductive: we will define the truth conditions of complex formulas in terms of the truth conditions of simpler ones in much the way with did with the definition of truth under an assignment of truth values to propositional variables in the case of propositional logic. We will begin with an account of the truth conditions of atomic formulas, and we will explain how to assign truth values to more complex sentences in a model relative to an assignment.
- Denotation
-
If
- Atomic Formulas
-
Example 6.11
Let
The evaluation of atomic formulas is similar when we use a diagram to specify a model.

Example 6.12 Consider a model
If a complex formula is constructed from simpler formulas by an application of a connective such as
- Negation
-
- Conjunction
-
- Disjunction
-
- Conditional
-
Example 6.13
Let
The situation is similar for diagramatic representations of a model:

Example 6.14 Consider a model
We now explain how to evaluate quantified formulas of the form
- Existential Quantification
-
- Universal Quantification
-
Example 6.15
Let
The situation is similar for diagramatic representations of a model

Example 6.16 Consider a model
Once we define what is for a formula
- Truth in a Model
-
A formula
- Logical Truth
-
A formula
One difference between propositional logic and quantificational logic is that we are not in a position to survey all interpretations of the language in order to determine whether a formula is a logical truth. There is an infinity of domains of discourse to consider and there are different interpretations available for the constants and predicates of the language available for each such domain. The generalization of the tableaux method will provide us with an indirect method for establishing the logical truth of a formula, but in the meantime, all we are in a position to do is to find a counterexample model when a formula is not a logical truth.
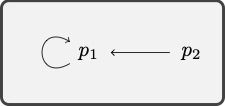
Example 6.17 The formula
The model depicted by the diagram verifies the antecedent of the conditional
The atomic formula
- Equivalence
-
Two formulas
We find ourselves in a similar situation. We are not yet in a position to establish that two formulas are logically equivalent, but if they are not, we may set out to find a counterexample in the form of a model in which one formula is true and the other one is false.
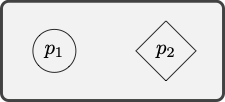
Example 6.18 The formulas
The model
The conjunction
The existential quantification
- Consistency
-
A set of formulas
If a set of formulas is consistent, then we are in a position to search for a model in which all of their members are true, but it is a different matter to conclusively establish that a set of sentences is inconsistent.
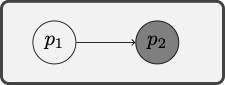
Example 6.19 The set of formulas
All these formulas are true in the model depicted by the diagram:
- Validity
-
An argument of quantificational logic is valid if, and only if, there is no model which all of its premises are true while its conclusion is false. Otherwise, the argument is invalid.
If an argument is not valid, then we are in a position to search for a model in which the premises are true and the conclusion is false. Otherwise, we will have to rely on a generalization of the tableaux method in order to establish validity.

Example 6.20 Consider the following argument:
The model depicted by the diagram verifies the premises of the argument but falsifies the conclusion.
The conditional
The negation
The existential quantification
Exercises
Determine whether each of the following expressions is an atomic formula of quantificational logic.
Determine whether each of the following expressions is a formula of quantificational logic.
Determine whether each of the following expressions is an abbreviation for a formula of quantificational logic.
Determine whether the following formulas contain a free occurrence of the variable
Determine whether the following formulas are open or closed. Justify your answers.
Determine which of the following formulas are true in the model: